A quelle distance peut-on voir un météore ?
>Je reçois un e-mail.
La plupart posent des questions de différents types, dont la plupart sont assez simples à répondre (en fait, on pourrait répondre à beaucoup de choses en cherchant sur Google, un indice). Mais parfois, je reçois une question à laquelle il est plus difficile de répondre, ou même une question à laquelle je me suis posé des questions mais que je n'ai jamais réussi à résoudre.
J'ai donc été assez intrigué lorsque j'ai reçu une question de Bad Reader Dean Lewis sur les météores. Lors de la pluie de météores des Perséides en 2018, il était loin de sa famille, séparés d'environ 1 000 kilomètres. S'il voyait un météore, était-il possible qu'ils puissent voir le même depuis leur lieu plus éloigné ?
La reponse courte est oui! La réponse longue est… maths. Des maths sympas et amusantes.
Et vu comment, lorsque cet article est publié, la pluie de météores annuelle des Géminides 2018 culmine ce soir, je pense qu'il est approprié de comprendre cela.
Cours accéléré d'astronomie : météores, météorites et météorites, oh mon Dieu !
Si la Terre était parfaitement plate, alors en principe, vous pourriez voir un météore jusqu'à n'importe quel bord de la Terre. Tant que vous êtes au-dessus du sol, même un tout petit peu, votre champ de vision atteint chaque centimètre carré de la planète de votre côté, de sorte que chaque météore est visible par tout le monde. En réalité, l'air n'est pas parfaitement transparent, donc à une certaine distance, vous regardez à travers tellement de boue que vous ne pouvez rien voir.
Cependant, la Terre n'est pas plate. Sérieusement! C'est rond. Et l'atmosphère l'entoure comme une coquille, s'amincit avec la hauteur et finit par s'épuiser ; cette hauteur dépend de votre définition de l'espace. Cependant, nous pouvons tricher un peu puisque nous connaissons la science : les météores comme ceux des averses ont tendance à brûler à environ 100 kilomètres au-dessus du sol. Cette hauteur dépend de beaucoup de choses, y compris la taille de la météoroïdes (les morceaux solides de débris interplanétaires traversant l'espace) sont, à quelle vitesse ils se déplacent, à quel angle ils pénètrent dans l'atmosphère, et ainsi de suite. Mais appelons ça 100 km.
Le météore le plus proche peut être de vous si vous êtes directement en dessous, puis il est à 100 km en ligne droite (à votre zénith). S'il brûle plus loin du zénith, alors il doit être plus loin de vous. Le plus loin que vous puissiez voir un météore, cela va de soi, c'est donc s'il est exactement à l'horizon.
La géométrie de celui-ci ressemble à ceci (remarque : PAS à l'échelle) :
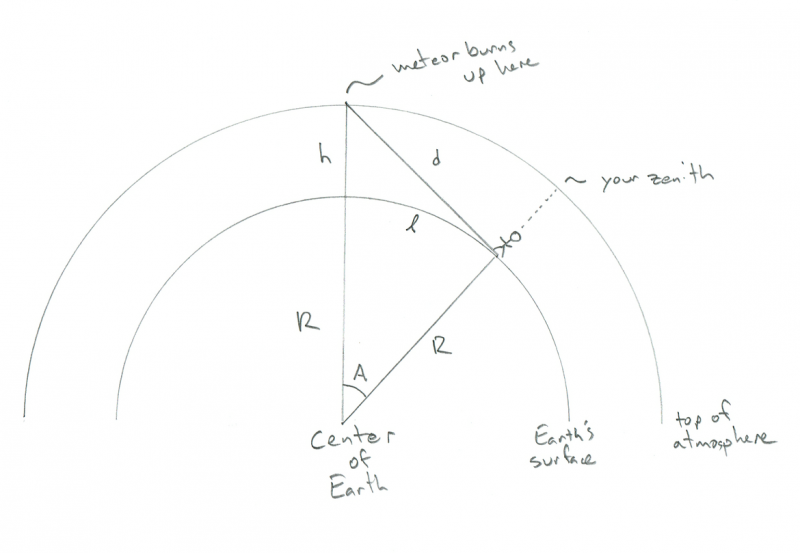
Schéma montrant la géométrie d'un observateur regardant un météore brûler. Crédit : Phil Plait
méprisable moi 3 médias de bon sens
Vous pouvez voir le petit bâton humain debout à la surface de la Terre incurvée - disons que c'est vous - avec l'atmosphère (également incurvée) au-dessus d'eux. Dans ce diagramme, R est le rayon de la Terre (6 4000 km), h est la hauteur à laquelle le météore brûle (100 km) et d est la distance entre vous et le météore. A est l'angle entre votre position sur la Terre et la position du météore au-dessus, et l cursif (comme dans la longueur) est la distance que vous devez parcourir pour que le météore soit directement au-dessus (je sais que cela semble être une chose étrange vouloir savoir, mais supportez-moi). Bizarrement, vous pouvez calculer tout ce dont vous avez besoin ici sans le savoir, mais allez, c'est cool de savoir à quelle distance se trouve le météore, non?
La clé de tout cela est de voir que l'angle entre le météore, vous et le centre de la Terre est un angle droit. C'est parce que le météore est à l'horizon tel que vous le voyez (ou, si vous préférez un jargon amusant, sur la ligne tangente du cercle intérieur où R l'intersecte). Cela fait du triangle un triangle rectangle, et si vous vous souvenez de vos maths de lycée, cela signifie que vous pouvez trouver tous les côtés et tous les angles !
Rappelles toi le théorème de Pythagore ? Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des deux autres côtés*. Dans notre triangle, l'hypoténuse est R+h, et les autres côtés sont R et d.
Alors
(R+h)2= d2+ R2
ou en multipliant le membre de gauche (utilisez DÉJOUER ):
R2+ 2Rh + h2 = d2+ R2
Résolvez pour d pour voir à quelle distance le météore est de vous. Notez que R2 est des deux côtés, alors annulez-les pour obtenir
ré2= 2Rh + h2
Ou alors
seigneur des mouches niveau scolaire
d = racine carrée(2Rh + h2)
Eh bien, nous connaissons tous ces chiffres! Plug-n-chug, bébé :
d = racine carrée (2 x 6 400 x 100 + 10 000) = 1 136 km
Ah ! Cela signifie que si vous voyez un météore à l'horizon, il se trouve à plus de 1 100 kilomètres ! C'est un long chemin, et techniquement le plus loin, vous pouvez voir un météore du sol.
Trouvons maintenant le cursif l. Nous devons d'abord connaître l'angle A. Cela nécessite une certaine trigonométrie. Il y a beaucoup de identités de déclenchement vous pouvez utiliser pour comprendre cela, mais mon préféré†est que dans un triangle rectangle, le sinus d'un angle est la longueur du côté opposé divisée par la longueur de l'hypoténuse. Donc, si nous obtenons ce rapport, nous pouvons prendre le sinus inverse (ou arcsinus) pour obtenir l'angle.
sin (A) = d / (R + h)
alors
A = sans-1(j / R + h)
Plug-n-chug à nouveau, et j'obtiens A = 10°. C'est une bonne partie de la surface de la Terre !
Et maintenant, nous pouvons obtenir l cursif. Il y a 360° autour de la Terre, et la circonférence de la Terre est de 2 x pi x rayon = 40 192 km, donc il y a
40 192 km / 360° = 112 kilomètres par degré
ce qui signifie, à son tour, 10° = 1 120 kilomètres. C'est assez proche de d, ce qui n'est pas trop surprenant. Les dessins sont exagérés, mais en réalité la coquille d'air au-dessus de nous est petite par rapport à la taille de la Terre. Si je faisais les dessins à l'échelle, vous verriez que d et l sont vraiment assez proches en longueur.
OK, alors pourquoi suis-je tout chaud et ennuyé de me trouver ? A cause de la question initiale ! Si vous avez oublié après tous ces calculs, c'est à quelle distance deux personnes peuvent-elles être et voir toujours le même météore ?
Eh bien dans ce cas le météore serait directement entre eux, et sur chacun de leurs horizons respectifs. Cette géométrie ressemble à ceci :
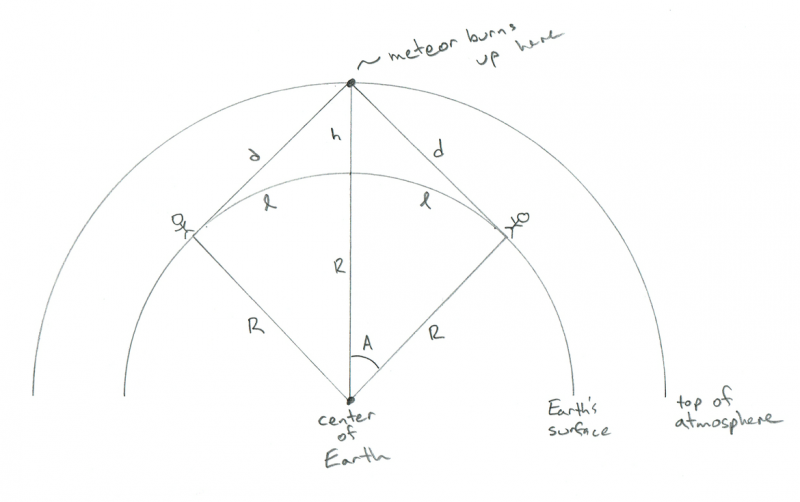
Schéma montrant la géométrie de deux observateurs observant un météore brûler exactement entre eux. Crédit : Phil Plait
AHA ! Maintenant tu vois pourquoi je veux moi ! La distance entre les deux personnes n'est que de 2 x l ! Alors maintenant, nous avons la réponse :
616 signification du nombre angélique
Pour que deux personnes voient le même météore, elles ne peuvent pas être distantes de plus de 2 x 1 120 = 2 240 kilomètres. Par exemple, c'est assez proche de la distance entre Washington, DC et Denver. Wow.
Incidemment, pour un changement de perspective (littéralement), cela signifie que du point de vue du météore, il peut voir une étendue de la Terre de 2 240 kilomètres de large (comme dans DC sur le flanc oriental de la Terre et Denver sur le flanc ouest). C'est plutôt cool.
Et cela nous amène à la vraie réponse à la question de Dean : s'il était à 1 000 km de sa famille, alors oui, techniquement, ils pourraient voir le même météore. Et ça ?
Maintenant, cela suppose à nouveau que l'air est parfaitement clair et tout cela, ce qui en réalité est essentiellement impossible. Donc, ce calcul représente une situation idéale (y compris l'idée que le météore est exactement entre eux).
Soyons plus réalistes. Disons que le météore brûle dans le ciel à une altitude de 45° au-dessus de l'horizon pour les deux observateurs. À quelle distance seraient-ils l'un de l'autre ? Eh bien, encore une fois, en supposant que le météore soit exactement entre eux, la géométrie ressemble plus à ceci :
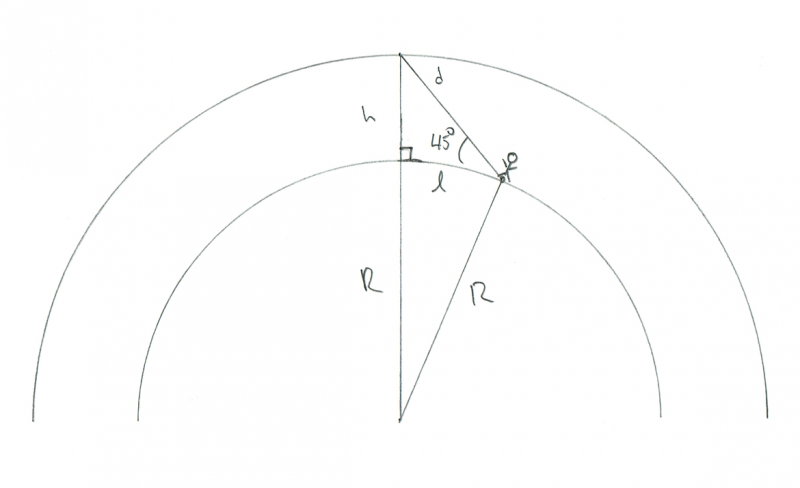
Schéma montrant la géométrie d'un observateur observant un météore brûlant à 45° au-dessus de l'horizon. Crédit : Phil Plait
C'est en fait plus difficile à résoudre, mais je connais une autre astuce : si nous supposons que l est petit, alors la courbure de la Terre ne sera pas importante. Par exemple, si je veux connaître la distance entre deux arbres dans mon jardin, je me fiche que la Terre soit courbée. Sur une si petite distance, je peux supposer que c'est plat. Faisons cette hypothèse ici.
Dans ce cas, nous avons un autre triangle rectangle, mais cette fois l'angle droit est celui sous le météore. Je l'ai même étiqueté dans le diagramme avec le petit truc de notation carrée. Donc, si c'est un angle de 90° et que notre angle avec le météore est de 45°, alors le dernier angle (du météore à l'observateur) est également de 45°. Cela signifie que ce doit être un triangle isocèle, donc l et h sont identiques ! Puisque nous savons que h est de 100 km, alors l doit en faire autant.
Et cela signifie que la distance entre nos deux observateurs est le double, soit 200 km.
Incidemment, dans ce cas, la distance au météore est d'environ 141 km. Je vais laisser confirmer cela comme exercice pour le lecteur.
En principe, cela signifie que si vous connaissez la hauteur de l'horizon d'un météore et l'altitude à laquelle il a brûlé, vous pouvez calculer sa distance (ou si vous connaissez la distance, vous pouvez obtenir sa hauteur). Ce trig est assez compliqué, cependant, et je pense que je vous ai jeté assez de maths pour aujourd'hui.
Mais c'est cool de penser qu'un peu de maths au lycée peut avoir une application aussi amusante. Et j'avoue que c'est poétique et romantique de savoir que, tant que la séparation n'est pas trop loin, il est possible de partager voir une étoile filante avec quelqu'un d'autre. Quelle belle pensée.
* Dans Le magicien d'Oz , l'épouvantail s'est trompé après il a un cerveau.
† De cours J'ai une identité de trig préférée. Quel est ton?